Il y aura en 2023 quatre éclipses : deux de Soleil et deux de Lune
| Date | Type | Visibilité |
| 20 avril 2023 | Éclipse de Soleil, successivement annulaire, totale et annulaire | Invisible en Belgique |
| 5 mai 2023 | Éclipse de Lune par la pénombre | En partie visible en Belgique |
| 14 octobre 2023 | Éclipse annulaire de Soleil | Invisible en Belgique |
| 28 octobre 2023 | Éclipse partielle de Lune | Visible en Belgique |
I – 20 avril 2023 – Éclipse de Soleil, successivement annulaire, totale et annulaire, invisible en Belgique
| Phase | Temps universel | Longitude | Latitude |
| Commencement de l’éclipse | 01h34,4 | 075 38 E | 40 18 S |
| Commencement de l’éclipse annulaire | 02h37,1 | 063 15 E | 48 32 S |
| Commencement de l’éclipse centrale | 02h37,1 | 063 37 E | 48 27 S |
| Commencement de l’éclipse totale | 02h37,3 | 067 57 E | 47 29 S |
| Eclipse centrale au midi apparent local | 03h55,6 | 120 52 E | 14 50 S |
| Maximum de l’éclipse | 04h12,6 | 124 49 E | 10 36 S |
| Fin de l’éclipse totale | 05h55,5 | 173 43 E | 04 14 N |
| Fin de l’éclipse centrale | 05h56,6 | 178 49 W | 02 55 N |
| Fin de l’éclipse annulaire | 05h56,7 | 178 34 W | 02 53 N |
| Fin de l’éclipse | 06h59,4 | 167 29 E | 11 12 N |
La carte ci-jointe montre la région où l’éclipse est observable. L’explication des codes utilisés se trouve en bas de page.
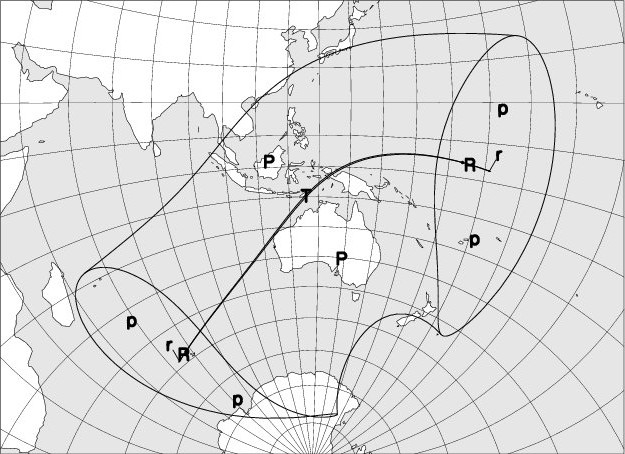
La durée de la phase de totalité le long de la ligne de centralité atteindra un maximum de 1m 21s en un point situé par 126° de longitude est et 10° de latitude sud. La durée de la phase annulaire le long de la ligne de centralité sera maximale à la fin de l’éclipse (9s).
II – 5 mai 2023 – Éclipse de Lune par la pénombre, en partie visible en Belgique
| Phase | Temps universel | Longitude | Latitude | Angle de position | Hauteur à Uccle |
| Entrée de la Lune dans la pénombre | 15h12,1 | 129 39 E | 16 46 S | 072 E | – |
| Maximum de l’éclipse | 17h23,0 | 098 01 E | 17 15 S | 023 E | – |
| Lever de la Lune à Uccle | 19h20,5 | 069 38 E | 17 40 S | 337 E | 0 |
| Sortie de la Lune de la pénombre | 19h33,8 | 066 26 E | 17 42 S | 334 E | +02 |
La longitude et la latitude se rapportent au point de la Terre où la Lune se trouve à cet instant au zénith. L’angle de position est défini à partir de la ligne imaginaire qui relie le centre du disque lunaire au centre de l’ombre de la Terre. Il est mesuré au centre du disque lunaire, à partir du Nord, dans le sens inverse du mouvement des aiguilles d’une montre. Au début et à la fin des phases de pénombre et d’ombre, c’est l’angle de position du point de contact. La hauteur et les instants de lever et coucher de la Lune sont calculés pour son centre, sans tenir compte de la réfraction.
Grandeur de l’éclipse: 0,989, le diamètre du disque lunaire étant pris pour unité.
La carte ci-jointe montre la région où l’éclipse est observable. L’explication des codes utilisés se trouve en bas de page.
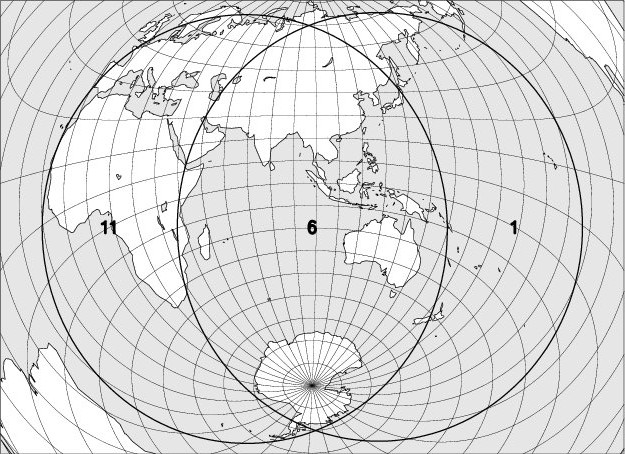
III – 14 octobre 2023 – Éclipse annulaire de Soleil, invisible en Belgique
| Phase | Temps universel | Longitude | Latitude |
| Commencement de l’éclipse | 15h03,8 | 132 32 W | 41 19 N |
| Commencement de l’éclipse annulaire | 16h10,2 | 146 54 W | 49 00 N |
| Commencement de l’éclipse centrale | 16h12,4 | 146 55 W | 49 21 N |
Eclipse centrale au midi apparent local |
17h36,6 | 087 40 W | 16 58 N |
| Maximum de l’éclipse | 18h03,4 | 082 20 W | 10 27 N |
| Fin de l’éclipse centrale | 19h46,8 | 029 23 W | 05 41 S |
| Fin de l’éclipse annulaire | 19h49,0 | 029 37 W | 06 03 S |
| Fin de l’éclipse | 20h55,3 | 045 01 W | 13 44 S |
La carte ci-jointe montre la région où l’éclipse est observable. L’explication des codes utilisés se trouve en bas de page.
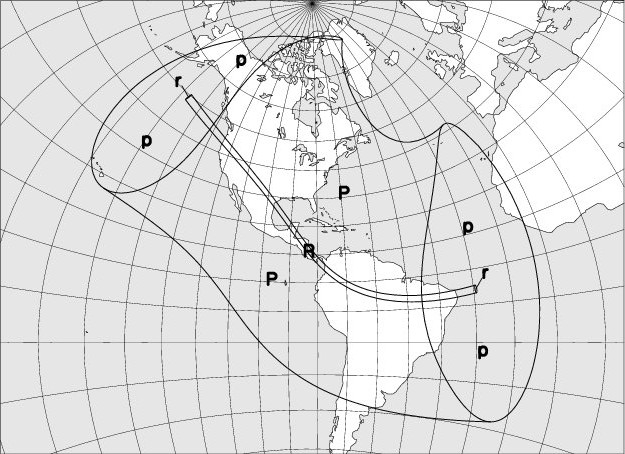
La durée de la phase annulaire le long de la ligne de centralité atteindra un maximum de 5m 13s en un point situé par 80° de longitude ouest et 8° de latitude nord.
IV – 28 octobre 2023 – Éclipse partielle de Lune, visible en Belgique
| Phase | Temps universel | Longitude | Latitude | Angle de position | Hauteur à Uccle |
| Entrée de la Lune dans la pénombre | 17h59,9 | 084 25 E | 13 31 N | 102 E | +16 |
| Entrée de la Lune dans l’ombre | 19h34,4 | 061 35 E | 13 55 N | 134 E | +30 |
| Maximum de l’éclipse | 20h14,0 | 052 02 E | 14 05 N | 155 E | +36 |
| Sortie de la Lune de l’ombre | 20h53,6 | 042 28 E | 14 15 N | 176 E | +42 |
| Sortie de la Lune de la pénombre | 22h28,3 | 019 37 E | 14 38 N | 208 E | +51 |
La longitude et la latitude se rapportent au point de la Terre où la Lune se trouve à cet instant au zénith. L’angle de position est défini à partir de la ligne imaginaire qui relie le centre du disque lunaire au centre de l’ombre de la Terre. Il est mesuré au centre du disque lunaire, à partir du Nord, dans le sens inverse du mouvement des aiguilles d’une montre. Au début et à la fin des phases de pénombre et d’ombre, c’est l’angle de position du point de contact. La hauteur et les instants de lever et coucher de la Lune sont calculés pour son centre, sans tenir compte de la réfraction.
Grandeur de l’éclipse: 0,128, le diamètre du disque lunaire étant pris pour unité.
La carte ci-jointe montre la région où l’éclipse est observable. L’explication des codes utilisés se trouve en bas de page.
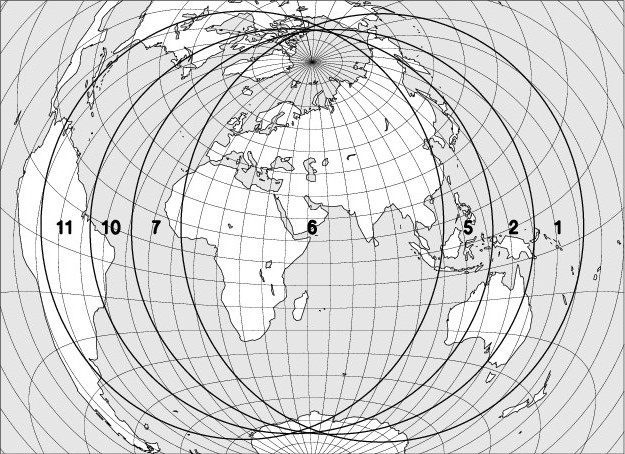
Explications :
Les codes utilisés sur les cartes pour indiquer la visibilité des éclipses de Lune sont: l’entrée dans la pénombre est visible dans les régions 1 à 6, l’entrée dans l’ombre dans les régions 2 à 7, le début de la totalité dans les régions 3 à 8. Les sorties de la totalité, de l’ombre et de la pénombre sont respectivement observables dans les régions 4 à 9, 5 à 10, et 6 à 11. Dans la région 6, on peut observer l’éclipse entière, dans les régions 5 à 7 les phases ombrales sont observables; dans les régions 4 à 8 la totalité est entièrement visible.
Sur les cartes de visibilité d’éclipses de Soleil, les codes suivants sont utilisés:
« P »: Eclipse partielle de Soleil, visible.
« p »: Eclipse partielle de Soleil, en partie visible.
« R »: Eclipse annulaire, dont la phase annulaire est entièrement observable.
« r »: Eclipse annulaire, dont la phase annulaire est partiellement observable.
« T »: Eclipse totale, dont la phase de totalité est entièrement observable.
« t »: Eclipse totale, dont la phase de totalité est partiellement observable.
Les données de base ayant servi à la rédaction du chapitre des éclipses ont été empruntées à l’intégration numérique DE405, aimablement mise à notre disposition par le Jet Propulsion Laboratory. Pour passer du Temps Terrestre (TT) au Temps universel (UT), la relation provisoire suivante a été utilisée:
UT = TT – 69,0 s
