In 2020, there will be six eclipses: two solar eclipses and four lunar eclipses
| Date | Type | Visibility |
| 10 January 2020 | Penumbral lunar eclipse | Visible in Belgium |
| 5 June 2020 | Penumbral lunar eclipse | Partially visible in Belgium |
| 21 June 2020 | Annular solar eclipse | Not visible in Belgium |
| 5 July 2020 | Penumbral lunar eclipse | Partially visible in Belgium |
| 30 November 2020 | Penumbral lunar eclipse | Not visible in Belgium |
| 14 December 2020 | Total solar eclipse | Not visible in Belgium |
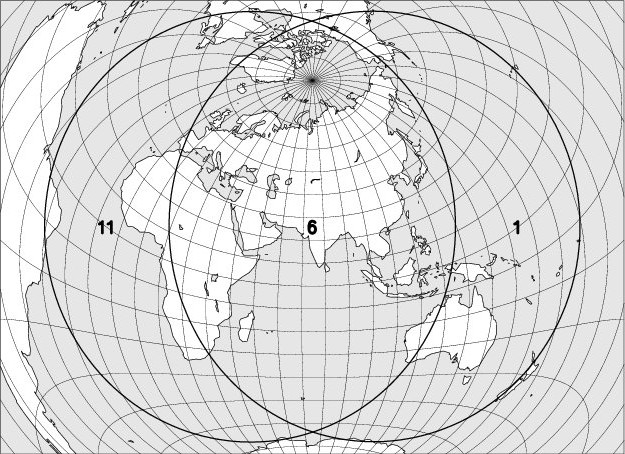
I – 10 January 2020 – Penumbral lunar eclipse, visible in Belgium
| Phase | Universal Time | Longitude | Latitude | Position angle | Altitude at Uccle/Ukkel |
| Penumbral eclipse begins | 17h05.7 | 104 15 E | 23 04 N | 136 E | +11 |
| Maximum of the eclipse | 19h10.1 | 074 23 E | 23 00 N | 183 E | +29 |
| Penumbral eclipse ends | 21h14.4 | 044 33 E | 22 56 N | 230 E | +48 |
The longitude and the latitude refer to the point on Earth where the Moon is at that time at its zenith. The position angle is defined from the imaginary line that connects the center of the lunar disc to the center of the Earth’s shadow. It is measured at the center of the lunar disc, from the North, in an anti-clockwise direction. At the beginning and at the end of the penumbra and shadow phases, it is the position angle of the contact point. The altitude and times of the Moon’s rise and fall are calculated for its center, without taking refraction into account.
Magnitude of the eclipse: 0.921, the diameter of the lunar disk being taken as the unit.
The map below shows the region where the eclipse is observable. The explanation of the codes used can be found at the bottom of the page.
II – 5 June 2020 – Penumbral lunar eclipse, partially visible in Belgium
| Phase | Universal Time | Longitude | Latitude | Position angle | Altitude at Uccle/Ukkel |
| Penumbral eclipse begins | 17h43.4 | 093 05 E | 21 15 S | 154 E | – |
| Maximum of the eclipse | 19h24.9 | 068 42 E | 21 27 S | 192 E | – |
| Moonrise at Uccle/Ukkel | 19h46.3 | 063 33 E | 21 30 S | 201 E | 0 |
| Penumbral eclipse ends | 21h06.5 | 044 18 E | 21 39 S | 229 E | +08 |
The longitude and the latitude refer to the point on Earth where the Moon is at that time at its zenith. The position angle is defined from the imaginary line that connects the center of the lunar disc to the center of the Earth’s shadow. It is measured at the center of the lunar disc, from the North, in an anti-clockwise direction. At the beginning and at the end of the penumbra and shadow phases, it is the position angle of the contact point. The altitude and times of the Moon’s rise and fall are calculated for its center, without taking refraction into account.
Magnitude of the eclipse: 0.593, the diameter of the lunar disk being taken as the unit.
The map below shows the region where the eclipse is observable. The explanation of the codes used can be found at the bottom of the page.
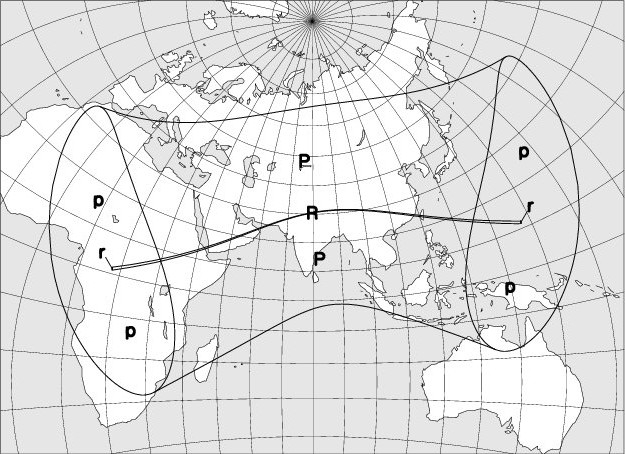
III – 21 June 2020 – Annular solar eclipse, not visible in Belgium
| Phase | Universal Time | Longitude | Latitude |
| Eclipse begins | 03h46.0 | 034 10 E | 01 08 S |
| Annular eclipse begins | 04h47.7 | 017 45 E | 01 07 N |
| Central eclipse begins | 04h48.4 | 017 48 E | 01 16 N |
| Central eclipse at the local solar noon | 06h41.4 | 080 07 E | 30 35 N |
| Maximum of the eclipse | 06h45.4 | 081 28 E | 30 46 N |
| Central eclipse ends | 08h31.7 | 147 35 E | 11 28 N |
| Annular eclipse ends | 08h32.3 | 147 39 E | 11 19 N |
| Eclipse ends | 09h34.1 | 131 12 E | 09 03 N |
Magnitude of the eclipse: 0.,995, the diameter of the solar disk being taken as the unit.
The map below shows the region where the eclipse is observable. The explanation of the codes used can be found at the bottom of the page.
The duration of the annular phase along the centrality line will reach its maximum at the beginning of the eclipse (1m 20s) and will reach a minimum of 33s at a point located at 82° of longitude east and 31° of latitude south.
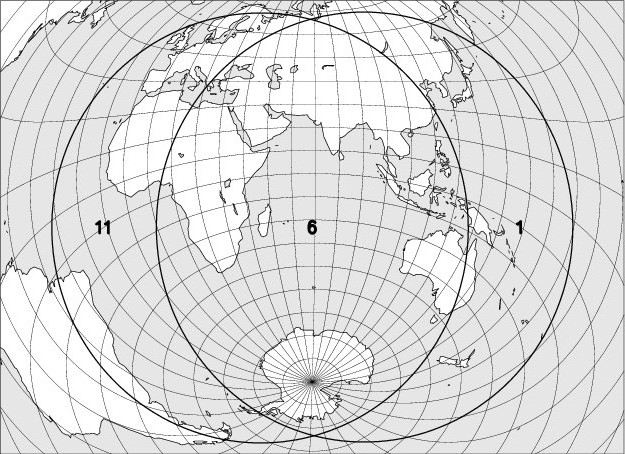
IV – 5 July 2020 – Penumbral lunar eclipse, partially visible in Belgium
| Phase | Universal Time |
Longitude | Latitude | Position angle |
Altitude at Uccle/Ukkel |
| Penumbral eclipse begins | 03h04.3 | 045 44 W | 24 04 S | 029 E | +02 |
| Moonset at Uccle/Ukkel | 03h23.9 | 050 26 W | 24 04 S | 024 E | 0 |
| Maximum of the eclipse | 04h29.8 | 066 17 W | 24 03 S | 360 E | – |
| Penumbral eclipse ends | 05h55.5 | 086 53 W | 24 02 S | 330 E | – |
The longitude and the latitude refer to the point on Earth where the Moon is at that time at its zenith. The position angle is defined from the imaginary line that connects the center of the lunar disc to the center of the Earth’s shadow. It is measured at the center of the lunar disc, from the North, in an anti-clockwise direction. At the beginning and at the end of the penumbra and shadow phases, it is the position angle of the contact point. The altitude and times of the Moon’s rise and fall are calculated for its center, without taking refraction into account.
Magnitude of the eclipse: 0.380, the diameter of the lunar disk being taken as the unit.
The map below shows the region where the eclipse is observable. The explanation of the codes used can be found at the bottom of the page.
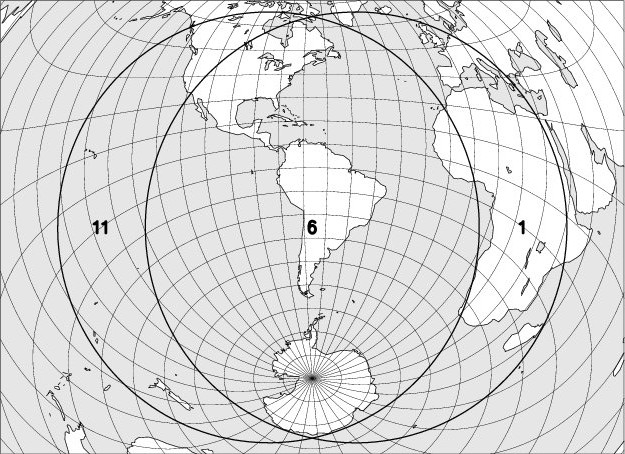
V. – 30 November 2020 – Penumbral lunar eclipse, not visible in Belgium
| Phase | Temps universel | Longitude | Latitude | Position angle |
Altitude at Uccle/Ukkel |
| Penumbral eclipse begins | 07h30.0 | 116 05 W | 20 28 N | 030 E | – |
| Maximum of the eclipse | 09h42.9 | 148 16 W | 20 45 N | 345 E | – |
| Penumbral eclipse end | 11h55.8 | 179 36 E | 21 01 N | 300 E | – |
The longitude and the latitude refer to the point on Earth where the Moon is at that time at its zenith. The position angle is defined from the imaginary line that connects the center of the lunar disc to the center of the Earth’s shadow. It is measured at the center of the lunar disc, from the North, in an anti-clockwise direction. At the beginning and at the end of the penumbra and shadow phases, it is the position angle of the contact point. The altitude and times of the Moon’s rise and fall are calculated for its center, without taking refraction into account.
Magnitude of the eclipse: 0.854, the diameter of the lunar disk being taken as the unit.
The map below shows the region where the eclipse is observable. The explanation of the codes used can be found at the bottom of the page.
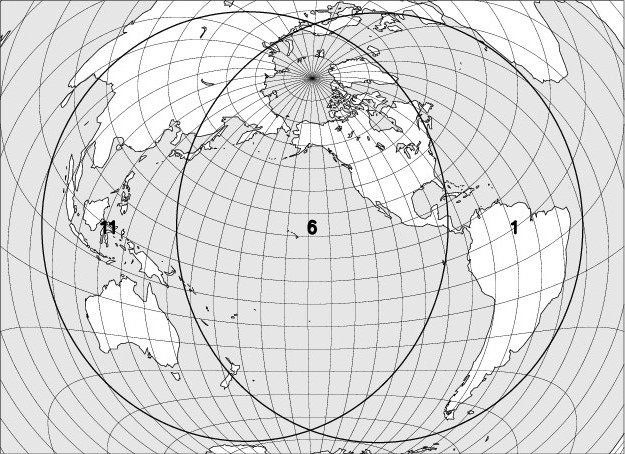
VI – 14 December 2020 – Total solar eclipse, not visible in Belgium
| Phase | Universal Time | Longitude | Latitude |
| Eclipse begins | 13h33.9 | 115 54 W | 02 00 S |
| Total eclipse begins | 14h32.5 | 132 30 W | 07 50 S |
| Central eclipse begins | 14h32.8 | 132 50 W | 07 46 S |
| Maximum of the eclipse | 16h10.1 | 069 29 W | 39 59 S |
| Central eclipse at the local solar noon | 16h18.2 | 065 49 W | 40 46 S |
| Central eclipse ends | 17h54.1 | 011 03 E | 23 37 S |
| Total eclipse ends | 17h54.3 | 010 42 E | 23 42 S |
| Eclipse ends | 18h53.1 | 006 15 W | 17 53 S |
The map below shows the region where the eclipse is observable. The explanation of the codes used can be found at the bottom of the page.
The duration of the totality phase along the centrality line will reach a maximum of 2m 14s at a point located at 68° of longitude west and 40° of latitude south.
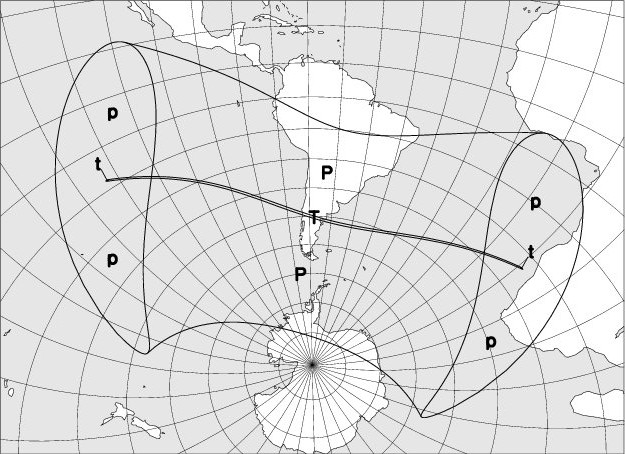
Explanations:
The codes used on the maps to indicate the moon eclipse visibility are: entry into the darkness is visible in regions 1 to 6, entry into the darkness in regions 2 to 7, the beginning of the totality in regions 3 to 8. The exits of the totality, the shadow and the penumbra are respectively observable in regions 4 to 9, 5 to 10, and 6 to 11. In region 6, the entire eclipse can be observed, in regions 5 to 7 the umbral phases are observable; in regions 4 to 8 the totality is fully visible.
On solar eclipse visibility maps, the following codes are used:
“P”: Partial eclipse of the Sun, visible.
“p”: Partial eclipse of the Sun, partly visible.
“R”: Annular eclipse, whose annular phase is fully observable.
“r”: Annular eclipse, whose annular phase is partially observable.
“T”: Total eclipse, whose totality phase is fully observable.
“t”: Total eclipse, whose totality phase is partially observable.
The basic data used to write the eclipse chapter were borrowed from the DE405 digital integration, kindly provided by the Jet Propulsion Laboratory. To move from Terrestrial Time (TT) to Universal Time (UT), the following provisional relationship was used:
UT = TT – 70.0 s
